Der Transistor einmal anders

Einführungen wie der Transistor funktioniert und Schaltbeispiele gibt es ja genug. Ich möchte gerne, da ich es früher immer vermisst habe, einen kleinen Beitrag leisten um ein wenig Licht in die Berechnung der Verstärkung zu bringen und welche physikalischen Naturkonstanten daran beteiligt sind.

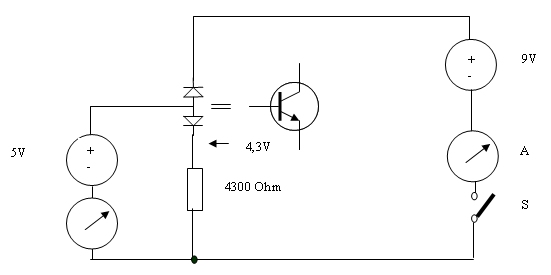
 Wir fangen mit der Diodenkennlinie an, da, wie Sie ja wissen, ein Transistor durch 2 Dioden, eine in Durchlaßrichtung, die Basis-Emitterdiode und die andere, die Basis-Kollektordiode in Sperrrichtung dargestellt werden kann. Folgende Schaltung: Ein npn- Transistor. Die Emitterbasisdiode in Durchlaßrichtung. Der Schalter S sei zunächst offen.

Das Amperemeter im Basisstromkreis zeigt etwa 1 mA an, da ja an der Diode eine Spannung von 0,7 V abfällt, wenn es ein Si-Transistor ist.. Das Amperemeter im Kollektorstromkreis zeigt natürlich nichts an. Schließt man nun den Schalter so zeigt das Amperemeter im Kollektorstromkreis 1 mA an und das Amperemeter im Basiskreis zeigt praktisch NULL an, vielleicht 2 µA, was ein Zeigerinstrument eben fast nicht darstellt.

Wir haben also gerade die Stromverstärkung des Transistors, mit einem Wert von 500 gemessen. Es fließen praktisch alle Elektronen, die vorher über die Basis geflossen sind über den Kollektor ab . Ich stelle mir den aktiven Transistorbereich sehr stark vergrößert vor wie folgt. Die Dotierung, also die gezielte Verunreinigung der n, p und n Schicht sei 1 Milliardstel.
Anders ausgedrückt jedes 1000ste Atom je Achse im Raum besteht nicht aus Silizium sondern aus z.B. Aluminium für das p-Gebiet und Phosphor für die n-Gebiete. Siehe auch: http://de.wikipedia.org/wiki/Dotierung

 
Die Basisdicke eines typ. Transistors kann z.B. 30 um sein. Ein Atom hat in etwa 0,3 nm Durchmesser. Über diese Basisdicke sind also 100000 Atome anzutreffen und nur 100 Stück sind nicht Silizium. Lokal gibt es also Stellen, die eine pos. oder neg. Ladung haben, also Elektronen anziehen oder abstoßen. Reines Silizium ist ja bei Raumtemperatur ein Isolator. Man dotiert um eine gezielte Leitfähigkeit zu erhalten.

 
Wieso fließen nun bei geschlossenem Schalter plötzlich fast alle Elektonen nicht über die Basis ab, sondern über den Kollektor?

Nun, der Kollektor liegt ja auf + 9V das ergibt über die Bassisdicke vereinfacht eine elektrische Feldstärke von E = (9-5) / 30e-6 = 130000 V/m. Das ist eine ordentliche Zugkraft! Würden Sie sich trauen bis auf 1 Meter an eine Hochspannungsleitung heranzugehen? Sicher nicht.

 
Alles was an Elektronen nicht zum Kollektor gelangt, fließt weiter über die Basis ab. Aber siehe weiter oben, wie wenig Elektronen das sind. Jetzt schauen wir uns einmal die Diodenkennlinie genauer an:

Es besteht folgender Zusammenhang zwischen Spannung und Strom (Siehe auch: http://de.wikipedia.org/wiki/Diode):

 
I = Is* (exp(U/(n*Ut)) -1) das ergibt z.B. diese Kennlinie für Is = 1e-8 A und n=1

Ut = k*T/q = 25,9 mV siehe weiter unten unter „innerer Emitterwiderstand"

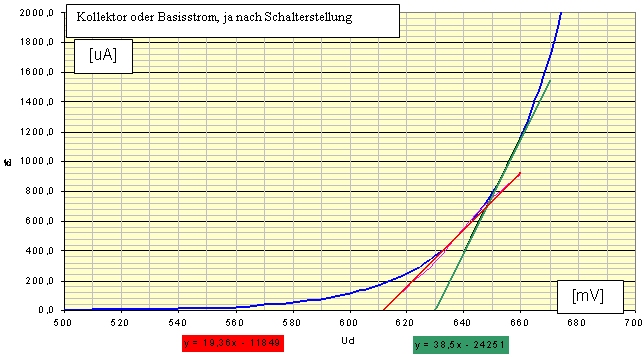
Sie sehen die rote und grüne Ausgleichsgerade, für den jeweiligen Arbeitspunkt = Tangente an die Diodenkurve. Im Arbeitspunkt bei 1000 uA = 1 mA beträgt die Steilheit 38,5 uA/mV = ~ 39 mA/V. Und bei 500 uA ~19,5 mA/V, also die Hälfte. Wenn man sich die Kurve näher ansieht, so erkennt man, dass es bei 2 mA entsprechend aussieht, 78 mA/V usw. Das leitet sich alles von der e-Potenzfunktion der Diodenkannlinie ab.

Jetzt kommt es schon bekannt vor: mA/V klingt nach Steilheit, egal ob Röhre oder Transistor. Die Verstärkung ist v = Steilheit * Arbeitswiderstand. Man erkennt auch, dass die Ausgleichsgerade sich nur für ca. 10 mV= 3,5 mVeff mit der Diodenkennlinie deckt, d.h. dass die lineare Aussteuerung nicht größer gewählt werden darf, da es sonst zu Verzerrungen der Kollektorstromes kommt und die will ja schließlich keiner.

 
Jetzt ein praktisches Beispiel in Emitterschaltung:

 
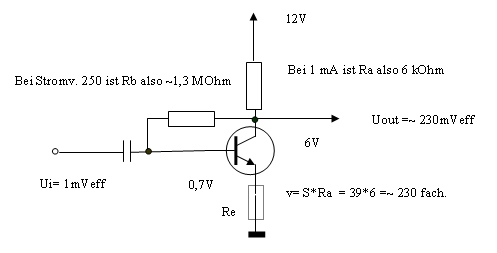
Ich persönlich verwende immer den Kehrwert der Steilheit, was dann die Dimension V/mA, also eines Widerstandes hat, der auch als „innerer Emitterwiderstand" Re bezeichnet wird, der bei 1 mA 25,9 Ohm beträgt. Siehe auch Ut, es ist nicht zufällig merkwürdig!!

Die Verstärkung ist dann einfach v= Ra / Re und ebenfalls ~230. Ich find's praktischer. Der Eingangswiderstand der Schaltung ist dann auch einfach ermittelt mit Ri = Re * Stromverstärkung = 26 * 250 = 6500 Ohm. Das stimmt auch, wenn im speziellen Fall nicht der Arbeitspunkteinstellwiderstand Rb mit etwa 1300 kOhm nicht wäre. An diesem liegt ja an einem Ende die Eingangsspannung, am anderen Ende die Ausgangsspannung, übrigens phasenverkehrt. Das ergibt einen Strom von Irb = (Uout - Uin)/Rb = (v +1 )Ui/Rb , was einem Widerstand der parallel zum Eingang liegt mit Rb/(v+1) also 1300/~230 = 5,7 kOhm. Der gemessene Eingangswiderstand wäre also 6500 // zu 5700 = ~ 3 kOhm. Wenn Sie also über einen Steuerwiderstand von 3 kOhm die Eingangsspannung zuführen, so sinkt die Verstärkung auf die Hälfte, durch diese Spannungsteilung.
Der Vorteil ist, dass Sie dadurch eine Gegenkopplung eingeführt haben, was die Verzerrungen bereits deutlich reduziert.

 Alle diese Berechnungen sind nicht exakt, da ja keine Vierpolparameter verwendet wurden. In der Praxis liegt die Genauigkeit dieser Berechnungsmethode aber besser als 5%, also für die Praxis weitaus mehr als ausreichend genau. Auch für Zwischenfrequenzen wenn Sie nicht gerade den OC45 aus den Anfangszeiten der Transistortechnologie verwenden. Übrigens: wenn Sie alle Widerstände um den Faktor 2 erhöhen, so ändert sich die Verstärkung nicht ein bisschen. Es spielt sich alles eben hochohmiger ab. Wenn Sie also Strom sparen wollen oder müssen....