Solarkonstante, Überlegungen zum Licht
von Heinz D.
1.
Die Solarkonstante = 1367W/m*m ist die Leistung, die pro Quadratmeter
von der Sonne (5600K, 555nm) auf die Erde gestrahlt wird. Am Boden
kommen je nach Wetter und Breitengrad etwa die Hälfte an (750W/m*m bis
1066W/m*m).
2. Die offizielle Umrechnung von Watt in Lumen/Lux
ist 1W = 683Lm = 683Lux/m*m (555nm, Wirkungsgrad = 100%). Diese
Rechnung mit pro Quadratmeter funktioniert bei quasi parallelen
Strahlen, Sonne -> Erde sehr gut. Somit werden am Boden 750W * 683Lx
= 512kLx bei 555nm erwartet. (Led-Lampen liegen mit 70Lm/W bei einem
Wirkungsgrad von ~10%. Glühlampen bei ~14Lm/W, ca. 2%)
3. Eine
BPW34 ist zwar eine kleine, aber sehr gut reproduzierbare Solarzelle
(mit ~0,9 Elektronen pro Photon). Im Datenblatt sieht man, dass
Ik=75nA/Lx bei 950nm nur ~33% bei 555nm (Sonne) entsprechen, also
Ik=25nA/Lx*512kLx=12.8mA.
4. Die maximale Leistung von
Solarzellen ist bei Ri=Ra: Pmax=U0/2*Ik/2 ! Im Gegensatz zu Batterien,
wo man die Energie auch zeitlich später abnehmen kann, muss bei
Solarzellen U0=2*Ulast sein, also ~3,2V. Ri begrenzt den Ladestrom
automatisch, leider wird in Ri die gleiche Energie (50%) in Wärme
umgesetzt. Eine Solar-Einzelzelle hat U0= 0,4V-0,7V.
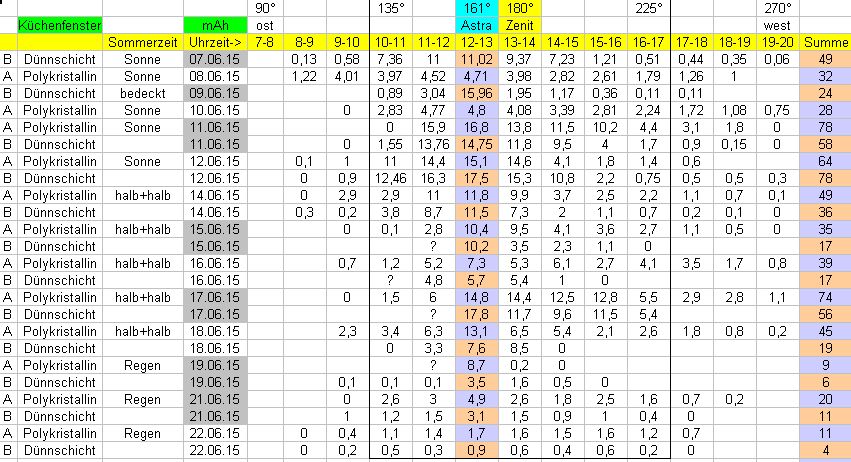
5. Praktische Versuche mit Gartensolarlampen:
A= 4 blaue polikristalline Zellen mit 20mm * 38mm = 760 mm*mm effektiv (schwarz aus 2005)
B= 4 braune Dünnschicht-Zellen mit 35mm * 40mm = 1400 mm*mm effektiv (bunt neu 2015)
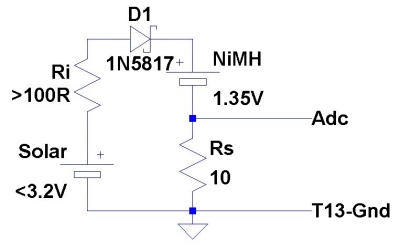
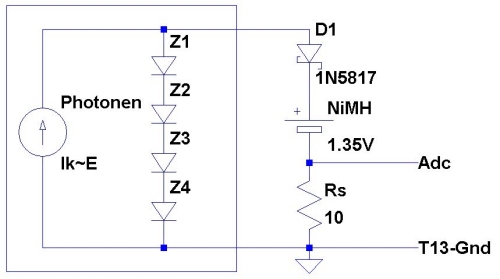
Eine
NiMh-Zelle (1,35V) wird über eine Schottkydiode (0,25V) und Rs=10R
geladen. In unseren Breiten werden Mittags kaum 200kLx erreicht. Die
Versuche wurden (reproduzierbar) in einem Astraspiegel vorgenommen:
19°ost und ~20° nach oben. Etwa 90% der Ladung wurde zwischen 11 und 16
Uhr erzielt, also +-37,5° vom Zenit um 13.30 (Sommerzeit).
6. Sparrow/T13 Solar-Logger
Der
Shuntwiderstand Rs=10R (Rs=12R, weil er gerade da lag) wird zwischen
B.4=U2 und Gnd angeschlossen. Mit dem Watchdog wird alle ~8s eine
Messung durchgführt, aufaddiert und ins EEPROM geschrieben. Leider lief
unser Watchdog (T13V+T13A) erheblich zu langsam (~9s) ! weswegen wir
die 1hconst auf 400 verringern mussten. Überschreitet die Spannung
300mV (30mA*10R), sollten Sie Rs etwas verkleinern, da die 300mV beim
Laden fehlen.
In EE-Zelle 1 steht die aktuelle Messstunde
(1...15). In EE 3+2 steht der Messzähler (Word = 0...1hconst). In
Vierer-Schritten (zwei Word) pro Stunde werden in EE 7+6 Mah und Mal in
EE 5+4 gespeichert. In EE 7+6 (B+A, F+E usw.) sind die geladenen mAh
direkt ablesbar. Aus EE 5+4 (9+8, D+C usw.) kann die Nachkommastelle
berechnet werden: Mal/Ifconst. Mit S1 werden alle EEPROM-Zellen auf 0
gesetzt. Mosi, Miso und Sck sind bewusst freigelassen, um das EEPROM
auszulesen.
P.S. Der Todesstrafe zweimal entronnen (nicht zur
Nachahmung). Während der Versuche wurde der T13 mehrmals zwischen
Messaufbau und Brenner umgesockelt, um das EEPROM auszulesen. Zweimal
wurde er dabei verkehrt herum eingesteckt (Brenner 5V, LiIon 3V). Nach
8s merkt man das erst, weil die Led nicht blitzt, er überlebte.
Download: solar-logger-bas-hex.zip
' Sparrow/T13 Solar-Logger (Zenit bei 7,5°ost = 13.30 Uhr Sommerzeit)
'
' Summierung bis zu 15 Stunden (6-21Uhr), 439.5 messungen/h = 1hconst
' Versuche zeigen, das schon nach 400 Messungen 1h um ist -> 1hconst=400, ggf. anpassen
'
' bei jeder Messung blitzt RED schwach
' mit S1 (8s festhalten) wird das EEPROM gelöscht, wenn RED schwach leuchtet
' gemessen wird an B.4=Ad2
'
' U = I*Rs
' ad = U*1023/Uref = I*Rs*1023/1100mV = I*Rs*0,93
' mit 1mA*1h -> 1h*1mA *Rs*0,93 = 1hconst*1mA *Rs*0,93 = mAh
' Ifconst = 1hconst*Rs*0.93
'
' Imax = Uref/Rs
' in Mah stehen die mAh (Word) berechnet zur Verfügung
' die Nachkommastelle kann berechnet werden: Mal / ifconst
' die erste EEPROM-Zelle kann zufällige Werte annehmen! und wird nicht genutzt
'-------------------------------------------------------------------------------
$regfile = "attiny13.dat"
$crystal = 1200000 '$prog &HFF , &H22 , &HFF , &H00 preserve EEPROM
$hwstack = 8 '32
$swstack = 8 '8
$framesize = 8 '16
$programmer = 19 'UsbAsp
Stop Ac :
U0 Alias Getadc(0)
Ddrb.0 = 0 : S1 Alias Pinb.0 : S1p Alias Portb.0 : S1p = 1 'pullup S1
Ddrb.3 = 0 : Red Alias Portb.3
Ddrb.4 = 0 : U2 Alias Getadc(2)
Config Watchdog = 8192 : Start Watchdog : Reset Watchdog
Config Adc = Single , Prescaler = Auto , Reference = Internal
Const 1hconst = 400 '3600s/8.192s=439.45
Const Ifconst = 3720 'Rs= 10R, Imax= 110mA
'Const Ifconst = 4464 'Rs= 12R, Imax= 91mA
Dim Mal As Word '
Dim Mah As Word '=1*mAh
Dim Messung As Word 'anzahl
Dim Stunde As Byte 'stunde
Dim Zeiger As Byte
Dim Zeigerh As Byte
Red = 1 'test
'-------------------------------------------------------------------------------
Readeeprom Stunde , 1 '1 bis 15
Readeeprom Messung , 2 'anzahl
If Messung > 1hconst Then : Messung = 0 : Stunde = Stunde + 1 : End If 'next h
If Stunde > 15 Then : Messung = 0 : Stunde = 1 : End If 'überlauf
If S1 = 0 Then : 'EE löschen
Messung = 0 :
For Stunde = 1 To 63 : Writeeeprom Messung , Stunde : Next
Stunde = 1 : Do : Loop Until S1 = 1 : End If 'S1 ?
Zeiger = Stunde * 4
Readeeprom Mal , Zeiger 'x*uAh, mAh=Mal/Ifconst
If Messung = 0 Then Mal = 0
If Mal = 65535 Then Mal = 0 'FFFF
Zeigerh = Zeiger + 2
Readeeprom Mah , Zeigerh 'mAh
If Messung = 0 Then Mah = 0
If Mah = 65535 Then Mal = 0 'FFFF
Mal = Mal + U2 'summierung
If Mal > Ifconst Then
Mal = Mal - Ifconst
Mah = Mah + 1 : End If
Messung = Messung + 1
Writeeeprom Stunde , 1 'EE 1
Writeeeprom Messung , 2 'EE 3+2
Writeeeprom Mal , Zeiger 'EE 5+4 ...
Writeeeprom Mah , Zeigerh 'EE 7+6 ...
Red = 0 'test
Powerdown :
Nop 'warte auf WD-Reset
'-------------------------------------------------------------------------------
End
Data "____S o l a r - L o g g e r ____"
'end program
Nachtrag
Wegen
Wind und Wetter wurden die Messungen hinters Küchenfenster (Doppelglas,
Richtung Astra) verlegt. Jede Glasscheibe reflektiert/dämpft im Mittel
8% (*2 ~16%). Die absoluten Zahlen sind nebensächlich, nur der Trend
ist entscheidend. Die Dünnschicht-Zellen (B) sind den polykristallinen
Zellen (A) etwa gleichwertig. Die blauen (A) scheinen schräg
einfallendes Licht besser zu nutzen.
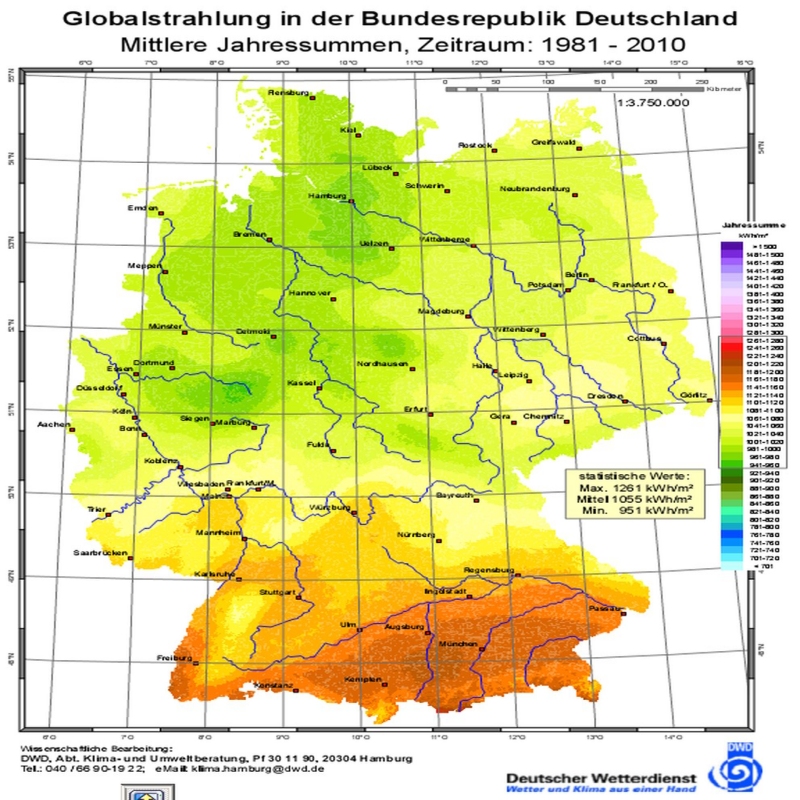
Beim DWD im Downloadbereich gibt es (freie) Karten. Das Ruhrgebiet ist nicht gerade sonnenverwöhnt.
Die Software musste angepasst werden:
S1
machte manchmal Schwierigkeiten und wurde entfernt. Ein T13 ab Werk
löscht das EEPROM mit erneutem flashen. Die Daten werden 1h im RAM
gehalten und dann erst ins EEPROM geschrieben. Trotzdem sind die Daten
der ersten acht EE-Zellen oft nicht zu gebrauchen!? die weiteren schon.
Wechsel Sie die Batterie nur unmittelbar nach erlöschen der Led.
Download: solar-logger7-bas-hex.zip
Fazit: Achten Sie beim Kauf darauf, das Sie 4 blaue oder 4,5 braune Solarstreifen pro Akku sehen.
--------
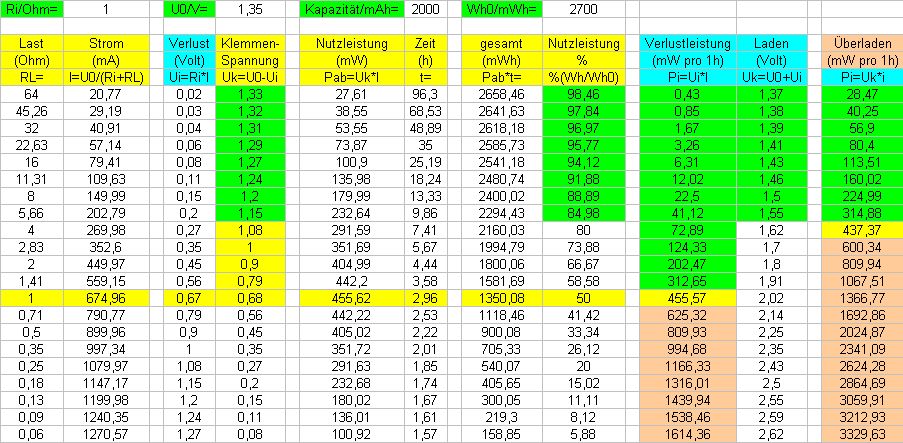
Pmax
für alle Hobbyisten ohne Elektrikerausbildung am Beispiel eines
Mignonakku 2000mAh. (viele Zahlen, gehen Sie in Gedanken Spalte für
Spalte durch und sehen den Praxisbezug)
Jede Spannungsquelle hat eine Leerlaufspannung U0 und einen Innenwiderstand Ri. Im
Beispiel wird U0=1,35V und Ri=1R angenommen. Man sieht das die
Klemmenspannung Uk bei RL <10R stark abnimmt. Bei Ri=RL ist Pab zwar
maximal, die Klemmenspannung ist jedoch schon zu klein. Mit einer
Kapazität von 2Ah dauert es ~3h bis die Zelle leer ist und 50% in der
Zelle in Wärme umgesetzt wird. Rechts sieht man, das mit kleinen
Strömen die meiste Energie entnommen wird (zeitlich später).
Mignonakkus können ~0,5W Wärme abstrahlen. Wird mit I=C/10 (<200mA)
geladen, dann ist überladen kein Problem. Schnelladegeräte müssen
demnach rechtzeitig abschalten. Beim Überladen entsteht ein
Innen-Gas-Druck von >80 Bar!
Wie bereits erwähnt, kann man Solarzellen die Energie nur sofort abnehmen, deshalb gilt bei Solar: Pmax bei Ri=RL
Nachtrag zur maximalen Leistung von Schimmi
Heinz D. schreibt in diesem schönen Artikel in Punkt 4.: Die maximale Leistung von Solarzellen ist bei Ri=Ra: Pmax=U0/2*Ik/2
Das
würde für einen ohmschen Widerstand als Innenwiderstand der Solarzelle
gelten. Dann ist die Ausgangskennlinie eine Gerade und das Rechteck mit
der groesten Flaeche. (Größtes Produkt aus beiden Kantenlängen die
Strom und Spannung darstellen -> höchste Leistung) liegt in der
Mitte der Linie.
Bei Solarzellen sieht die Linie aber doch eher
anders aus. Silizium-Solarzellen haben so ca 0,5V Leerlaufspannung
(temperaturabhängig ). Diese sinkt bei konstanter Beleuchtung zuerst
nur langsam mit steigender Last, um dann in eine
Linie überzugehen, die einen sich nur mehr gering zunehmenden
Strom zeigt. Die Maximale Leistung wird im Bereich des "Knicks"
erreicht und ist viel besser als U0/2*Ik/2 .
Nachtrag Klemmenspannung Uk und Kurzschlussstrom Ik von Heinz D.
Jede Spannungsquelle hat (für jeden gewählten Arbeitspunkt) eine Leerlaufspannung U0 und einen Innenwiderstand Ri!
Mit zunehmender Beleuchtung der Solarzellen sinkt Ri, das war mir bewusst, aber der Reihe nach:
Der Strom Ik ist proportional der Beleuchtungsstärke E (Photonen).
Die Urspannung U0 ist wie bei allen Silizium-PN-Übergängen eine e-Funktion und steigt um ~90mV/Dekade.
Also U0 etwa 800mV/512kLx, 710mV/51kLx, 620mV/5kLx, 530mV/500Lx usw. Somit ist Ri:
Ri=U0/Ik,
mit U0=e^x und Ik~E wird Ri= ~e^x/E,
mit e^x= nahezu konstant wird Ri= etwa K/E
Rechenbeispiel aus obiger Tabelle (Ri = delta U / delta I oder Ri = delta U / I):
11.06.(A) oder 13.6.(B) I~17mA, in beiden Fällen können wir von E>=100kLx und 4*0.8V=3.2V ausgehen, Risolar=1.6V/17mA=94R.
Ik WÄRE somit 3.2V/94R=34mA, WÜRDE dann jedoch zu 100% auf Ri in den Zellen verbraten.
22.06.(A) I~1.7mA, bei E>=10kLx und U0=3.2V-(4*90mV)=2.84V wird Risolar=(2.84V-1.6V)/1.7mA=730R.
Somit WÄRE Ik=2.84V/730R=3.9mA.
Um Hobbyisten nicht zu verwirren, bin ich vom Praxisbezug ausgegangen, ohne Ri berechnen zu müssen.
Ein Akku stellt mit seiner Diode eine nahezu konstante Lastspannung (Uk=1,6V, Ri~1R) dar.
U0solar ist zwar nicht konstant, ändert sich jedoch über die zwei interressanten Dekaden nur um +-90mV*Zellen.
Da Ri und I von E abhängen, wird der optimale Arbeitspunkt nahezu konstant (+-15%/2Dekaden) gehalten, wenn U0~2*Uk ist.
Ist U0 wesentlich größer oder kleiner, dann funktioniert diese 'Pmax-Automatik' nicht mehr.
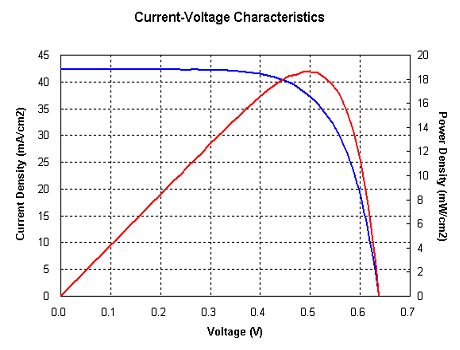
Nachtrag: Solarzellen-Kennlinie von Heinz D.
Sorry, ich muss mich berichtigen. Ich habe gefunden was offensichtlich mit 'Knick' gemeint war.
(Datenblatt monokristalline Zelle, polikristalline und amorphe Zellen sind nur wenig schlechter)
Ri
ist zwar ohmsch, jedoch nicht linear wie ich annahm, sondern der
differentielle Widerstand eines PN-Übergangs. Das optimale U-I-Paar
ergibt sich etwa 20% unter U0. An diesem Punkt geht die Solarzelle vom
~Konstantstrom (blaue, waagerechte Linie) in die ~Konstantspannung
über. Sinnvoll nutzbar ist nur der Konstantstrombereich.
Bitte ignorieren Sie die Berechnung für Ri für Solarzellen und die Folgerungen daraus!
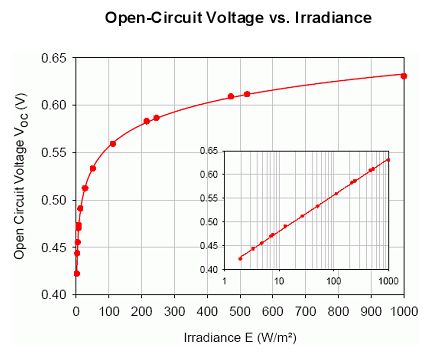
Weiterhin
wurde von mir U0 mit 800mV bei 512kLx angenommen, das Diagramm weist
~630mV bei 1kW/m*m = 683kLx aus. Diese Werte werden laut DWD nur im
Juni/Juli erreicht. Im Dezember/Januar werden im Mittel 71kLx erreicht
(~560mV). Zur Tag- und Nachtgleiche wird in etwa das 30-Jahresmittel
von ~330kLx erreicht (~610mV). In der kleinen logaritmischen
Darstellung sieht man, das die Änderung U0 bei etwa 70mV/Dekade liegt.
Die Aussage, das vier Solarzellen zum laden eines NiMH-Akkus erforderlich sind, kann so stehen bleiben. Rechnung:
U0-20% > 1.6V bei 683kLx = 630mV * 4 = 2.52V - 20% = 2.02V (Sommer)
U0-20% > 1.6V bei 330kLx = 610mV * 4 = 2.44V - 20% = 1.92V (Frühling/Herbst)
U0-20% > 1.6V bei 71kLx = 560mV * 4 = 2.24V - 20% = 1.79V (Winter)
So sind noch Spannungs-Reserven für die Dämmerung vorhanden.
Die
Temperaturabhängigkeit (-2mV/K) ist im Hochsommer ein Problem. Wird die
Solarbatterie um 50° wärmer, dann sinkt U0 von 630mV auf 530mV (-16%).
Manche Hersteller weisen im Datenblatt darauf hin. Zum Laden eines
12V-Autoakkus habe ich eine Solarbatterie mit 36 Zellen, U0=22,7V,
U0-20%=18.1V und einer Temperaturreserve U0-20% -16% = 15.2V > 13.6V
(bleiben Reserven für eine Diode). Sie ahnen nun, warum ich irrtümlich
annahm, das U0~2*Uk sein soll.
Mit
dem richtigen (idealen) Ersatzschaltbild wird es klarer. Hier sieht man
auch, dass eine unbelastete Solarbatterie den gesamten Fotostrom intern
verbraten muss.
Im obigen U-I-Diagramm kann man den
differenziellen Widerstand Ri=dU/dI bei Pmax mit 12R-15R ermitteln. RL
wäre dann 500mV/37mA=13.5R. Pmax bei Ri=RL stimmt demnach immer noch.
Betrieben werden Solarbatterien etwas unterhalb Pmax im
Konstantstrom-Bereich mit Spannungsreserve.
Ich hoffe nun, das
das Verhalten von Solarbatterien für jeden Hobbyisten nachvollziehbar
ist. Die Schmutzeffekte durch Kriechströme spielen hier keine große
Rolle und ich habe sie deshalb weg gelassen.
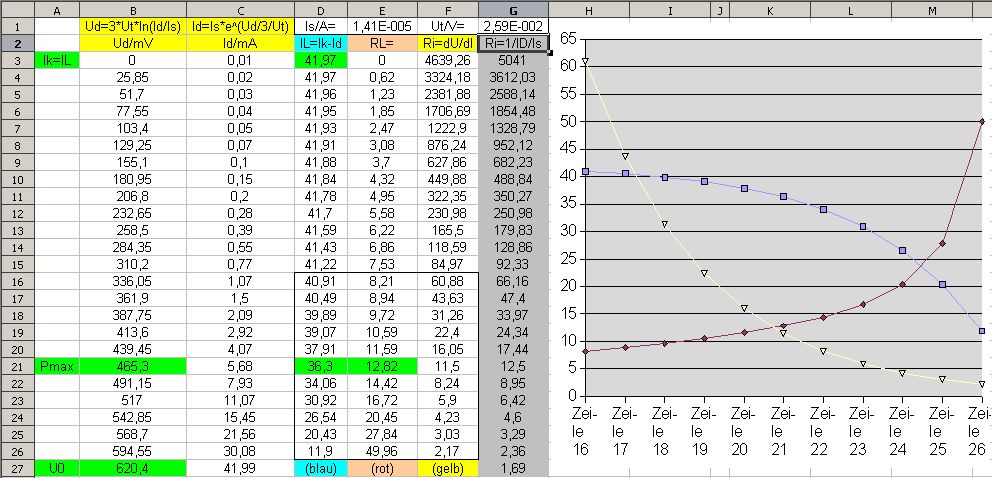
Obiges
U-I-Diagramm nachgerechnet. Die Tabelle gilt nur für einen
Arbeitspunkt: T=300K, E=1000W/m*m und nur einer einzigen
Materialkonstante IS. Jede Abweichung macht eine neue Rechnung
notwendig. Zum Glück bleibt die Tendenz gleich.
In Spalte B wird die Diffusionsspannug vorgegeben.
In Spalte C wird der zugehörige Diodenstrom berechnet, ID=IS*e^(UD/3/UT), mit UT=25.9mV bei T=300K.
In Spalte D ist IL=Ik-ID also der Rest, in Spalte E ist RL=UD/IL.
In Spalte F wird der differenzielle Ri=(U2-U1)/(I2-I1) aus zwei benachbarten Werten berechnet.
Das
Diagramm rechts zeigt die Werte in der Umrandung an. Bitte beachten
Sie, das T in UT und E in Ik steckt und somit Ri nicht allgemein
angegeben werden kann. Ausserdem ändert sich IS mit dem mechanischen
Aufbau und den Material-Eigenschaften. Am Ende des Tages sieht man in
Spalte G (grau), das Ri~1/(ID*IS) ist. Mein Herleitung hat es mit
Ri~K/E fast getroffen.